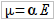Elektryczny moment dipolowy

Elektryczny moment dipolowy jest wektorową wielkością fizyczną, która opisuje dipol. Dipol jest układem ładunków elektrycznych o tej samej wartości lecz posiadających przeciwny znak. Elektryczny moment dipolowy μ wyraża się za pomocą równania:

gdzie q jest wartością elektrycznych ładunków punktowych, l odległością pomiędzy ładunkami. Wektor l ma zwrot od ładunku dodatniego do ujemnego. Gdy cząsteczka zawiera więcej atomów jej całkowity elektryczny moment dipolowy jest wektorową sumą wszystkich elektrycznych momentów dipolowych poszczególnych atomów i elektrycznych momentów dipolowych pochodzących od par atomów. Elektryczny moment dipolowy zależy od kształtu cząsteczki (np. cząsteczka CO2 posiada zerową wartość momentu dipolowego, natomiast cząsteczka SO2 posiada wypadkowy moment dipolowy o wartości 1.7 D).

Jednostką układu SI, za pomocą której wyrażany jest elektryczny moment dipolowy jest C·m (kulomb·metr), gdzie C = 6.24150·10¹⁸ e. Często stosowaną zamiennie jednostką elektrycznego momentu dipolowego jest debaj (D), który ma wartość równą 3.33564·10^-30  C·m.

Energia potencjalna oddziaływania dwóch dipoli elektrycznych o momentach dipolowych μ₁ i μ₂, które znajdują się w odległości r wyraża się równaniem (ε_o – przenikalność dielektryczna późni):

dla oddziaływania krańców dipoli o różnoimiennym ładunku, oraz:

dla oddziaływania bocznego dipoli, tak, że nakładają się na siebie ładunki różnoimienne. Dla analogicznego oddziaływania dipoli lecz nakładania się równoimiennych ładunków energia potencjalna ma ten sam wyraz, lecz przeciwny znak.

Oddziaływanie jon-dipol występuje pomiędzy jonem a cząsteczką polarną. Energię potencjalna oddziaływań pomiędzy jonem o ładunku q będącym w odległości r od dipola μ opisuje równanie:

Jest ono spełnione tylko wtedy, gdy jon i dipol leżą wzdłuż tej samej osi. Oddziaływanie przyciągające odpowiada za rozpuszczanie związków jonowych w rozpuszczalnikach polarnych. 

Jeżeli cząstka posiadająca ładunek, na przykład kation zbliży się do cząstki obojętnej, to może zmienić jej gęstość elektronową, cząstka ta uzyskuje wtedy indukowany moment dipolowy. Energię potencjalną oddziaływania obydwu cząstek opisuje równanie:

gdzie α jest polaryzowalnością o wymiarze m³ opisaną równaniem:

gdzie α' jest polaryzowalnością o wymiarze C·m²·V^-1.

Również cząsteczka posiadająca moment dipolowy może powodować w cząsteczce obojętnej indukowany moment dipolowy. Energia potencjalna takiego oddziaływania opisana jest równaniem:

gdzie α jest polaryzowalnością cząsteczki niepolarnej, μ jest momentem dipolowym cząsteczki polarnej. 

Energia potencjalna dla oddziaływań jon-dipol indukowany i dipol-dipol indukowany nie zależy od temperatury. Oddziaływania jon-dipol indukowany i dipol-dipol indukowany są słabe w porównaniu z oddziaływaniami jon-dipol. 

Polaryzowalność jest to wielkość fizyczna określająca zdolność odkształcenia rozkładu ładunku w cząsteczce pod wpływem zewnętrznego pola elektrycznego, definiuje się ją jako współczynnik proporcjonalności pomiędzy natężeniem tego pola a elektrycznym momentem dipolowym przez to pole indukowanym. Zależność tą opisuje równanie:

gdzie E jest natężeniem zewnętrznego pola elektrycznego, α jest polaryzowalnością. Polaryzowalność jest na ogół wielkością anizotropową tj. zależną od orientacji osi cząsteczki względem kierunku pola.

Zmiana polaryzacji powoduje powstawanie indukowanego indukowanego elektrycznego momentu dipolowego. Całkowita polaryzowalność α jest sumą polaryzowalności elektronowej α_e, jonowej α_a i polaryzacji orientacyjnej (dipolowej) α_o:

Polaryzowalność elektronowa α_e określa zdolność do deformacji powłoki elektronowej atomu pod wpływem zewnętrznego pola elektrycznego. Polaryzowalność elektronową dla niespolaryzowanych cząsteczek opisuje równanie:

gdzie e jest ładunkiem elektronu, m jego masą, ω₀ jest częstością własną (rezonansową) elektronu związanego atomem. 

Polaryzowalność jonowa α_j jest związana z przesunięciem w różne strony jonów dodatnich i ujemnych w polu elektrycznym, wskutek czego w sieci krystalicznej powstaje elektryczny moment dipolowy. Polaryzowalność związków jonowych opisuje równanie:

gdzie N jest ilością cząsteczek w jednostce objętości, q ładunkiem jonu zaś u całkowitym przemieszczeniem jonów dodatnich i ujemnych.

Polaryzowalność orientacyjna (dipolowa) αo związana jest ze zjawiskiem ustawienia przez zewnętrzne pole elektryczne trwałych dipoli w substancji polarnej zgodnie z kierunkiem linii sił pola. Polaryzowalność orientacyjną dla cząsteczek posiadających trwały moment dipolowy określa równanie:

gdzie μ jest elektrycznym momentem dipolowym cząsteczki, k_B stałą Boltzmana, T temperaturą.

Polaryzowalność orientacyjna występuje dla niskich częstości, do mikrofalowych, natomiast polaryzowalność elektronowa występuje dla najszerszej granicy częstości od zakresu widzialnego do nadfioletu. Wysokie częstości drgań powodują, że dipole nie nadążają za zmianami pola elektrycznego. Elektrony są najlżejsze i nadążają za tymi zmianami, stąd dla częstości optycznych występuje wyłącznie polaryzacja elektronowa. Do opisu ilościowego polaryzacji dielektryka stosuje się wektor polaryzacji określony równaniem:

gdzie: p_ei jest momentem elektrycznym i-tego dipola, V objętością dielektryka, N liczbą cząsteczek dipola w tej objętości. 

Z polaryzowalnością ściśle wiążą się wielkości takie jak przenikalność dielektryczna oraz współczynnik załamania światła.

Dla atomów, których elektrony są słabiej związane z jądrem polaryzowalność jest większa, nierzadko elektrony walencyjne mają największy wkład do polaryzowalności, tak więc im większy atom, tym większe prawdopodobieństwo jego polaryzacji. Dla cząsteczki indukowany moment dipolowy jest wielkością tensorową ponieważ nie jest on równoległy do natężenia pola elektrycznego. Dzięki istnieniu zjawiska polaryzowalności możliwe jest wykonanie widm spektroskopowych cząsteczek, które nie posiadają trwałego elektrycznego momentu dipolowego – zajmuje się tym spektroskopia Ramana.

Elektryczny moment dipolowy obliczany jest metodami chemii kwantowej jako średnia wartość momentu dipolowego w danym stanie, zgodnie z I postulatem mechaniki kwantowej, który mówi o tym, że stan cząstki określa funkcja falowa:

zależna od położenia x i czasu t. Operator momentu dipolowego i sam moment dipolowy nie zależą od wyboru układu współrzędnych tylko w przypadku molekuły obojętnej.

W metodzie Hartree-Focka elektryczny moment dipolowy jest sumą momentu dipolowego jąder i elektronów. Moment dipolowy jądra oblicza się stosując przybliżenie Borna-Oppenheimera, a moment dipolowy elektronów zgodnie z regułami Slatera-Condona. Polaryzowalność dipolową można obliczyć dwiema metodami:

• metodą sumy po stanach – polaryzowalność dipolową oblicza się stosując rachunek zaburzeń. Równanie energii n-stanu cząstki w jednorodnym polu elektrycznym zawiera człony energii cząstki, na którą nie działa pole elektryczne, człon energii oddziaływania pola elektrycznego z trwałym momentem dipolowym cząsteczki oraz energię oddziaływania pola elektrycznego z indukowanym momentem dipolowym
• metodą pola skończonego – wykonuje się obliczenia energii a z niej polaryzowalności, następnie wybiera się układ współrzędnych i przykłada pole. Realizacją sposobu tych obliczeń jest dodanie do hamiltonianu członu -μF, czyli uwzględnienie położenia układu w jednorodnym polu elektrycznym. Pewnym paradoksem obliczeń teoretycznych polaryzowalności jest fakt, że użycie bardzo dobrej bazy funkcyjnej nie daje wcale lepszych wartości, wręcz przeciwnie. Powodem jest dodany do hamiltonianu operator oddziaływania z polem elektrycznym. Tak więc obliczenia polaryzowalności w niezbyt dobrej bazie funkcyjnej dają przeważnie dość dobre wartości. Tak jest w przypadku obliczeń wariacyjnych. W przypadku obliczeń perturbacyjnych do drugiego rzędu sytuacja ta nie pojawia się. Poprawka trzeciego rzędu może dawać już pogorszenie wyników obliczenia polaryzowalności w bardzo dobrej bazie funkcyjnej.

Literatura:

1. K. Pigoń, Z. Ruziewicz: Chemia fizyczna T. 2 Fizykochemia molekularna, Wydawnictwo Naukowe PWN, 2011

2. L. Piela: Idee chemii kwantowej, Wydawnictwo Naukowe PWN, 2011

Potencjał korelacyjno-wymienny B3LYP

Teoria funkcjonałów gęstości (DFT – Density Functional Theory) jest zbiorem metod obliczeniowych chemii kwantowej bazującej na gęstości elektronowej stanu podstawowego badanego układu. Powyższe zdanie jest treścią pierwszego twierdzenia Hohenberga-Kohna, które wraz z drugim twierdzeniem Hohenberga-Kohna, mówiącym o tym, że dla energii stanu podstawowego minimum energii występuje dla rzeczywistej gęstości elektronowej stanu podstawowego, stanowią podstawę założeń metod opartych na funkcjonałach gęstości elektronowych. Metody te są cenną alternatywą metod bazujących na funkcjach falowych. Najbardziej popularną realizacją metod DFT jest metoda Kohna-Shama, której istotą jest zastąpienie oddziaływań pomiędzy elektronami koncepcją nieoddziałujących wzajemnie (ale oddziałujących z jądrami i polem zewnętrznym) elektronów, poruszających się w efektywnym potencjale. Potencjał ten należy dobrać tak, aby gęstość nieoddziałujących elektronów była równa gęstości rzeczywistej stanu podstawowego układu. Wyróżnić można trzy główne rodzaje metod obliczeniowych DFT: LDA (Local Density Approximation) traktująca układ jako jednorodny gaz elektronowy, NLDA (non-Local Density Approximation) uwzględniająca nielokalność, GC (Gradient Corrected) czyli metody przybliżeń gradientowych oraz metody hybrydowe, które zawierają (jako składową) również metodę Hartree-Focka. Metody obliczeniowe DFT mogą być stosowane do większości układów. W przeciwieństwie do metod ab initio stosowane są z powodzeniem do obliczeń związanych z metalami przejściowymi, czyli w sytuacjach, gdzie metoda Hartree-Focka zawodzi z powodu małej różnicy energii między orbitalami HOMO i LUMO. Niektóre z metod hybrydowych, takie jak B3LYP używane są często do obliczeń reakcji chemicznych, natomiast potencjał MPW1K zaprojektowany został do obliczeń związanych z kinetyką chemiczną. Główną zaletą metod DFT jest czas obliczeń, który porównywany jest z czasem obliczeń metodą Hartree-Focka, tak więc ta sama moc obliczeniowa komputera pozwala na dokładniejsze obliczenia w tym samym czasie. Złożoność obliczeniowa metod DFT wynosi N³ natomiast metod ab initio N⁴, gdzie N jest liczbą funkcji bazy. Dokładność obliczeń DFT wynika z uwzględnienia korelacji elektronowej. Istotnym problemem metod funkcjonałów gęstości jest problem doboru danej metody obliczeniowej do konkretnego problemu, duże problemy z uwzględnieniem oddziaływań dyspersyjnych, w przypadku metody LDA bardzo duże błędy w obliczaniu energii wiązań (nawet do 40 kcal/mol) oraz problem z opisem stanów wzbudzonych. Opisu stanów wzbudzonych można dokonać metodami funkcjonałów gęstości zależnymi od czasu – TDDFT (Time Dependent Density Functional Theory). Opisem matematycznym metod obliczeniowych DFT jest funkcjonał. Energia obliczona tymi metodami jest funkcjonałem gęstości elektronowej (a ta jest funkcją zmiennych x, y, z). Niezależnie od ilości elektronów gęstość elektronowa zależy zawsze tylko od tych trzech zmiennych, tak więc aparat matematyczny nie komplikuje się przy zwiększeniu ilości elektronów. Głównym celem metod DFT jest znalezienie wartości funkcjonału, ponieważ jego postać nie jest jawna – ma charakter nielokalny. Poszukiwanie wymaga przybliżeń, tak więc dana metoda charakteryzuje się zastosowaniem określonej metody przybliżenia funkcjonału. Nierzadko stosuje się złożony aparat matematyczny tylko po to, aby jak najbardziej zbliżyć się do wyników zgodnych z doświadczeniem. Równanie określające energię w metodach DFT wygląda następująco:

gdzie T jest energią kinetyczną elektronów, E_ne energią elektrostatycznego przyciągania elektronu i jądra, J energią elektrostatycznego odpychania elektronów, natomiast E_xc energią korelacyjno-wymienną. Wartość każdego z tych członów (potencjałów) jest odrębnym problemem, który należy rozwiązać. Pierwsze trzy potencjały można z dość dobrym przybliżeniem określić przy użyciu metod ab initio bądź metod półempirycznych. Człon ostatni określany jest jako człon energii korelacyjno-wymiennej, która powoduje spore trudności w zdefiniowaniu. Energia korelacyjno-wymienna określa jaki wpływ elektronów na siebie ma ich indywidualne zachowanie, oraz uwzględnia fakt, że elektrony powinny unikać się z powodu odpychania elektrostatycznego oraz zakazu Pauliego (ta sama współrzędna spinowa). Czym jest energia korelacyjno-wymienna próbują wyjaśnić następujące metody (LDA, NLDA, GC), każda z nich w inny sposób definiuje jak dany elektron „widzi” inny elektron. Energia korelacyjno-wymienna składa się z części korelacyjnej E_c oraz części wymiennej E_x (energia ta wyraża się przez spinorbitale Kohna-Shama analogicznie do spinorbitali Hartree-Focka w metodzie HF), której postać analityczna jest znana dla układu jednorodnego. Równania opisujące energię korelacji mają charakter przybliżony i opierają się na parametryzacjach wyników symulacji QMC (Quantum Monte Carlo). Energia wymienna pełni ważniejszą funkcję niż energia korelacyjna.

Równanie na energię korelacyjno-wymienną w przypadku najbardziej popularnego potencjału hybrydowego B3LYP (Becke 3-term correlation functional; Lee, Yang, and Parr exchange functional) wygląda następująco:

gdzie E_xc^LSDA jest energią korelacyjno-wymienną LSDA, a_o(E_x^HF – E_x^LSDA) jest a_o-procentową różnicą między energią Hartree-Focka i energią wymienną LSDA, a_xE_x^B88 jest a_x-procentową energią wymienną Beckego z poprawkami gradientowymi, a_cE_c^LYP jest a_c-procentowym członem korelacyjnym Lee-Yang-Parr-a, parametry a_o, a_x oraz a_c są parametrami dostosowanymi eksperymentalnie. Tak więc potencjał B3LYP jest taką mieszanką potencjałów, aby wyniki były jak najbardziej zgodne z doświadczeniem. Ogólnie rzecz biorąc potencjał hybrydowy B3LYP przy bazie funkcyjnej 6-31G(d) lub lepszej jest dobrym wyborem do obliczania większości układów, szczególnie w przypadku cząsteczek organicznych. Gorzej jednak opisuje zachowanie się cząsteczek metaloorganicznych (odwrotnie niż potencjał hybrydowy BLYP). B3LYP daje również dobre wyniki w przypadku obliczeń reakcji chemicznych. Reasumując, potencjał korelacyjno-wymienny B3LYP cechuje się tym, że daje najlepsze wyniki w zastosowaniu dla szerokiej grupy układów molekularnych, jest więc bardzo uniwersalny.



Literatura:
1. K. Pigoń, Z. Ruziewicz: Chemia fizyczna T. 2 Fizykochemia molekularna, Wydawnictwo Naukowe PWN, 2011
2. L. Piela: Idee chemii kwantowej, Wydawnictwo Naukowe PWN, 2011